Authors: Simon Schrodi, Danny Stoll, Binxin Ru, Rhea Sanjay Sukthanker, Thomas Brox, and Frank Hutter
TL;DR
We take a functional view of neural architecture search that allows us to construct highly expressive search spaces based on context-free grammars, and show that we can efficiently find well-performing architectures.
NAS is great, but…
The neural architecture plays a major role for performance. Many works manually crafted architectures, e.g., He et al., CVPR 2016; Vaswani et al., NeurIPS 2017 or automatically searched for them, e.g., Kitano, Complex System 1990; Zoph & Le, ICLR 2017. Latter falls under the realm of neural architecture search (NAS). Despite the fact that NAS is a heavily-researched field with over 1000 papers over the last couple of years Deng & Lindauer; Literature overview 2022; White et al., arXiv 2023, NAS has primarily been applied to over-engineered, restrictive search spaces (e.g., cell-based ones) that did not give rise to truly novel architectural patterns.
Hierarchical search spaces are a promising step towards overcoming these limitations, while keeping the search space of architectures more controllable compared to global search spaces. We take up this idea and propose an universal search space design framework to construct such hierarchical search spaces.
Functional view on NAS
Before diving into the construction mechanism, we would like to note that NAS work typically view neural architectures as computational graphs:

While this is very illustrative, it is more challenging to handle. Thus, we consider the equivalent functional representation of neural architectures:
Sequential(Residual(conv, id, conv), Residual(conv, id, conv), linear)
where the functions conv, id, linear have an arity of 0 and Sequential, Residual have both an arity of 3. We refer to the former as primitive functions, as they apply a function, e.g., convolution, on the data. We refer to the latter as topological functions, as they define the topological/functional structure of the computational block. For instance, Residual has two paths: (1) two subsequent convolutional blocks (conv) and (2) a skip connection (id).
The main benefit of the functional representation is its close connection to the way we implement neural architectures in code and to strings, which we will leverage in our construction mechanism next.
Construction mechanism based on context-free grammars
Context-free grammars (CFGs) are a powerful mechanism for specifying (hierarchical) languages. In a nutshell, a CFG consists of production rules that define how sequences of symbols – so-called terminals and nonterminals – can be recursively combined to form valid strings of a language from a start symbol. They are one if not the fundamental building block in the design of programming languages and compiler construction. While CFGs entail much more, we want to keep it brief here and refer interested readers to, e.g., Niklaus Wirth’s “Compiler Construction”.
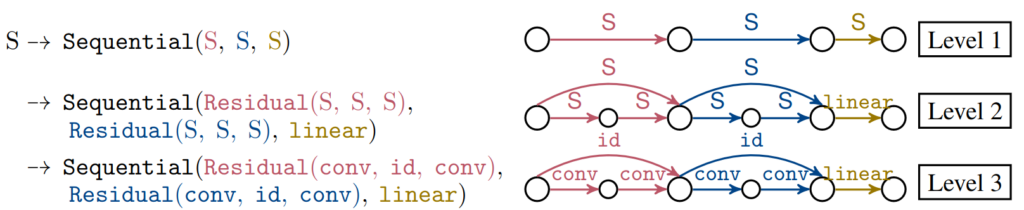
Our idea is to use CFGs to define how simple functions (primitive & topological functions) can be composed. Let’s consider the following CFG in extended Backus-Naur form [Backus, ICIP 1959]:
S -> Sequential(S,S,S)| Residual(S,S,S)|conv|id|linear
Here, S is the (nonterminal) start symbol and Sequential, Residual, conv, id, linear are terminals.
The figure below shows how we can derive the function composition from above and makes the connection to its computational graph representation explicit.
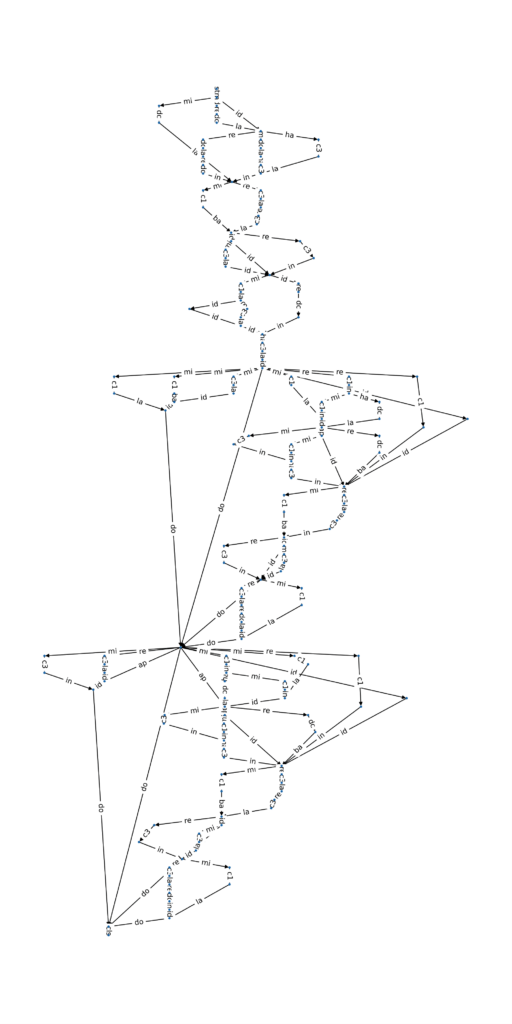
While this mechanism is already very powerful, there are several things missing that one may desire. We extended the CFGs with additional mechanisms to handle flexible spatial resolution flow, incorporation of user-specific constraints, and fostering regularity (i.e., re-use of architectural blocks). These mechansims let us construct entire neural architectures from top to bottom, while ensuring their validity (i.e., no resolution mismatches and the input is connected with the models’ output). Below is such a discovered neural architecture:
We refer readers interested in more details in our enhancements to our paper. Note that these enhancements only cover a fraction of all possible ones and there is a lot left on the table to study in future work.
Search strategy
Expressive (hierarchical) search spaces present challenges for NAS search strategies due to their huge size. We find that many previously proposed methods, e.g., gradient-based ones, do not scale to them without any novel adaptation. To search, we propose a novel Bayesian optimization strategy Bayesian Optimization for Hierarchical Neural Architecture Search (BOHNAS).
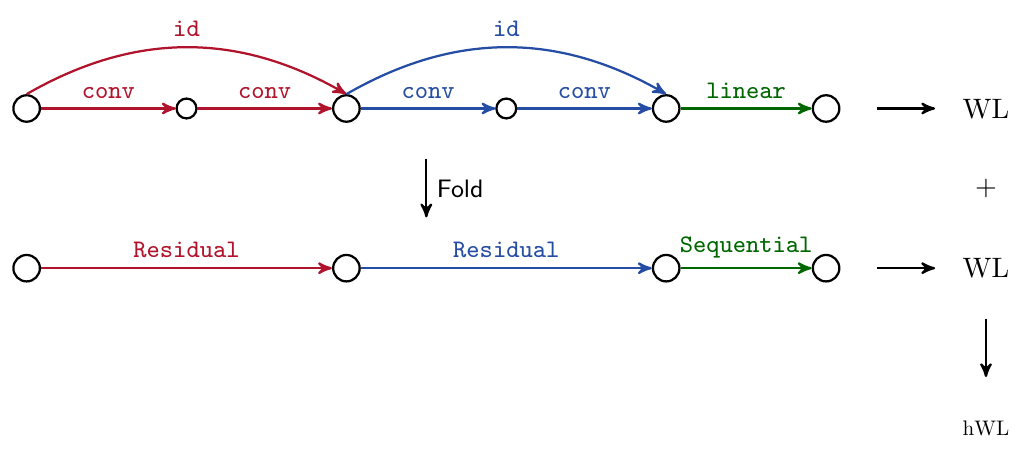
The main two components are a hierarchical kernel that constructs a kernel upon different granularities of the neural architectures to improve performance modeling (see the figure below for an intuition how it works) and adopt ideas from grammar-guided genetic programming.
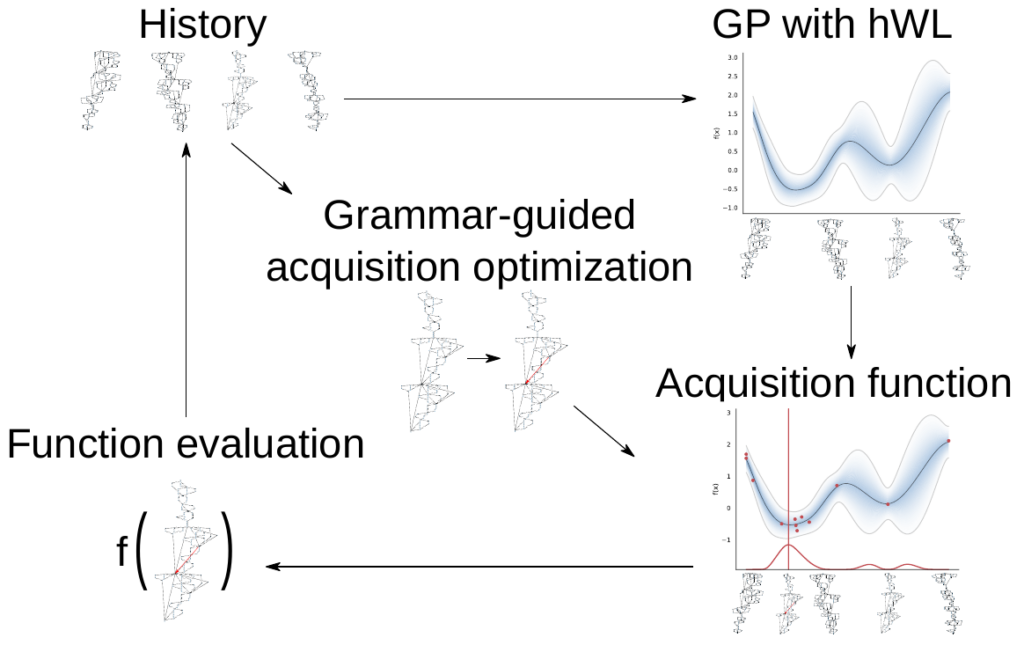
Our hierarchical kernel hierarchically constructs a kernel upon various granularities of the architectures. In essence, it loosely inverts the hierarchical construction mechanism in its kernel design!
Experimental results
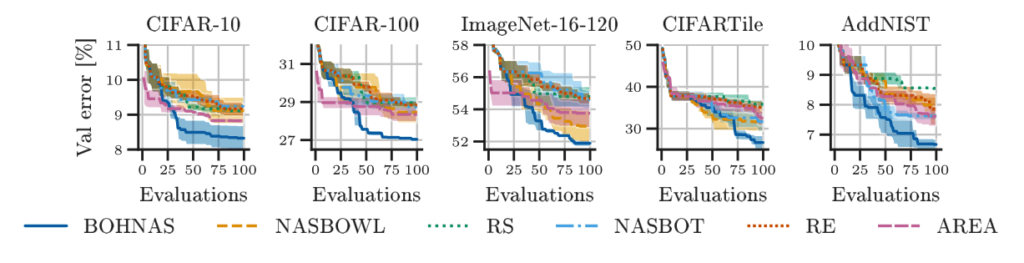
We conducted extensive experiments and found that NAS research should go beyond its restrictive search spaces to large, flexible search spaces, such as our hierarchical search spaces.
Specifically, we found that our method outperforms common baselines and finds indeed well-performing neural architectures across search spaces and datasets, often yielding superior performance

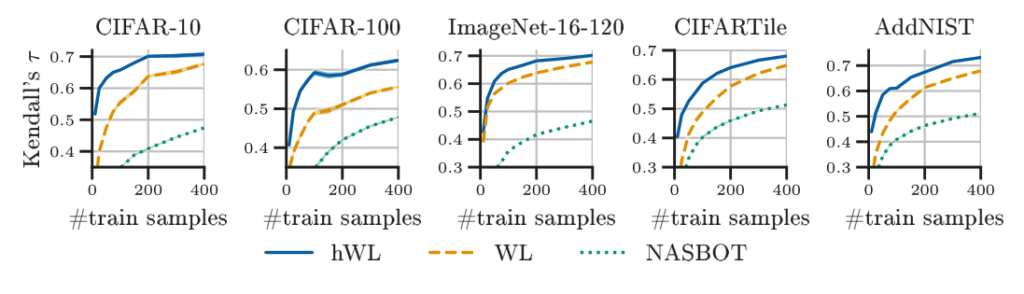
The hierarchical kernel design of BOHNAS is an important ingredient of its performance.
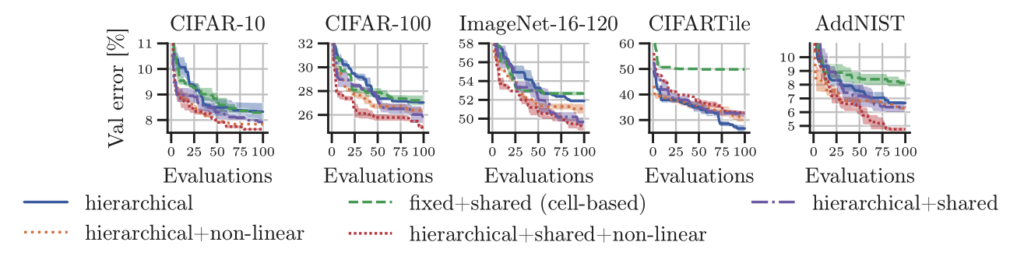
Indeed, these discovered neural architectures outperform those from a popular cell-based search space. Interestingly, promoting regularity at the cell-level and flexibility at the macro-level yielded the best-performing neural architectures:
Lastly, we note that our search space design framework can also be used to search for transformers for generative language modeling. Below, we show the found nanoGPT model (with embedding dimensionality of 192) that is trained on Shakespearean works following Andrej Karpathy:

Paper & Code
If you are interested in more details, feel free to check out our paper.
If you are eager to dive into the nitty-gritty and search neural architectures yourself, feel free to check out our code.
References
He et al., CVPR 2016 He, Kaiming, et al. “Deep residual learning for image recognition.” CVPR 2016.
Vaswani et al., NeurIPS 2017 Vaswani, Ashish, et al. “Attention is all you need.” Advances in neural information processing systems 30 (2017).
Kitano, Complex System 1990 Kitano, Hiroaki. “Designing neural networks using genetic algorithms with graph generation system.” Complex System 1990.
Zoph & Le, ICLR 2017 Zoph, Barret, and Quoc V. Le. “Neural architecture search with reinforcement learning.” ICLR 2017.
Deng & Lindauer; Literature overview 2022 Difan Deng and Marius Lindauer. [https://www.ml4aad.org/automl/literature-on-neural-architecture-search/](https://www.ml4aad.org/automl/literature-on-neural-architecture-search/) 2022.
White et al., arXiv 2023 White, Colin, et al. “Neural architecture search: Insights from 1000 papers.” arXiv 2023.
Backus, ICIP 1959 Backus, John W. “The syntax and the semantics of the proposed international algebraic language of the Zurich ACM-GAMM Conference.” ICIP Proceedings. 1959.