In many real world scenarios, deep learning models such as neural networks are deployed to make predictions on data coming from a shifted distribution (aka covariate shift) or out-of-distribution (OOD) data not at all represented in the training set.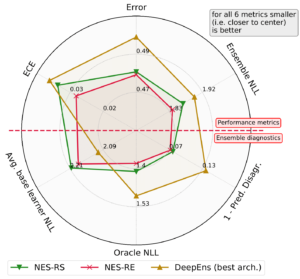
Examples include blurred or noisy images, unknown objects in images or videos, a new frequency band in audio signals, etc., and for many applications, such as medical imaging, the model confidence or uncertainty on such data can be crucial. The figure below shows a concrete example from Ilg et al., where the optical flow (middle) between two successive images (one of them on the left) is predicted. The model’s estimated uncertainty is represented as a heatmap (right) and assigns a higher uncertainty to the optical flow in the shadow of the car (see the red arrow), whereas the car and the pedestrian are estimated with higher confidence. Ideally, in the case of covariate shift the model would become more uncertain of its predictions as the accuracy degrades and for OOD data the model would be maximally uncertain of its predictions. This way, it would know what it does not know. However, this is not the case in practice. Usually neural networks are not well-calibrated, making overconfident predictions or assigning arbitrary classes to OOD data (see Ovadia et al.).
Ensembles of neural networks achieve superior performance compared to stand-alone networks not only in terms of predictive performance, but also in terms of uncertainty calibration and robustness to such shifts in distribution. Diversity among networks is believed to be key for building strong ensembles, but typical approaches, such as deep ensembles (Lakshminarayanan et al.), only ensemble the predictions coming from the same neural network architecture as follows:
- Independently train multiple copies of a fixed architecture with random initializations.
- Create an ensemble by averaging outputs, i.e. predicted distribution over the classes (in the case of classification).
It is natural to ask whether we can find better ensembles by also changing the architecture, and whether we can design an automated method for finding the right architectures to ensemble. In our Neural Ensemble Search (NES) paper, we answer both of these questions (with a ‘yes’). We investigate ensembles of different neural network architectures and we use neural architecture search (NAS) to construct such ensembles automatically. Our approach for finding base learner architectures that optimize ensemble performance consists of the following two steps:
- Pool building: build a pool of K base learners with potentially different architectures, where each network is trained independently on the training set.
- Ensemble selection: select M base learners from the pool to form an ensemble that minimizes the validation loss.
For step 2, we use forward step-wise selection without replacement (Caruana et al.): given the pool, start with an empty ensemble and add to it the network from the pool which minimizes the ensemble loss on the validation set. We repeat this without replacement until the ensemble is of size M.
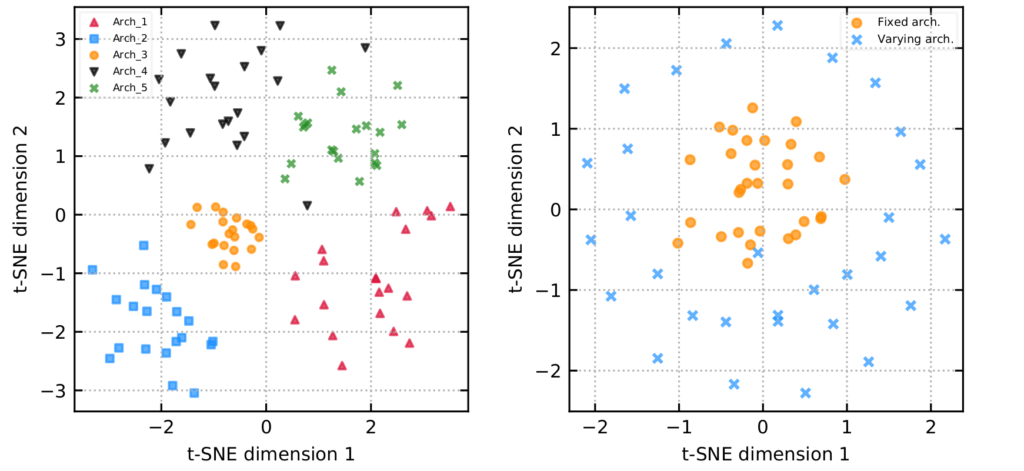
Visualizing predictions of varying vs. fixed architectures using t-SNE
Before jumping into the different ways we construct the pool in step 1, let’s firstly visualize the predictions of varying vs. fixed network architectures. The figure on the left below shows the t-SNE projections of the predictions of 5 different architectures, each trained with 20 different initializations, while the figure on the right shows the predictions of base learners with varying architectures (found by NES) vs. with a fixed architecture (deep ensemble of an optimized architecture). We observe clustering of predictions made by different initializations of a fixed architecture, while predictions from different architectures are positioned far from each other, suggesting that base learners with varying architectures explore different parts of the function space.
Constructing a pool of different architectures using NES
We consider two options for building a pool of size K that we will use later for selecting the ensemble base learners:
- NES-RS is a simple random search (RS) based approach, where we build the pool by sampling K architectures uniformly at random.
- NES-RE uses regularized evolution (RE) to build the pool by evolving a population of architectures.
The figure below illustrates the NES-RE routine. NES-RE starts with a randomly initialized population and at each iteration forward step-wise selection is applied in order to select an ensemble. Then a parent architecture is sampled from this ensemble and is mutated to yield a child architecture. The child is then added to the population and the oldest network is removed, keeping the population size fixed. This process is repeated until the computational budget K is reached, and the overall history is returned in the end as the pool.
Ensemble adaptation to dataset shift
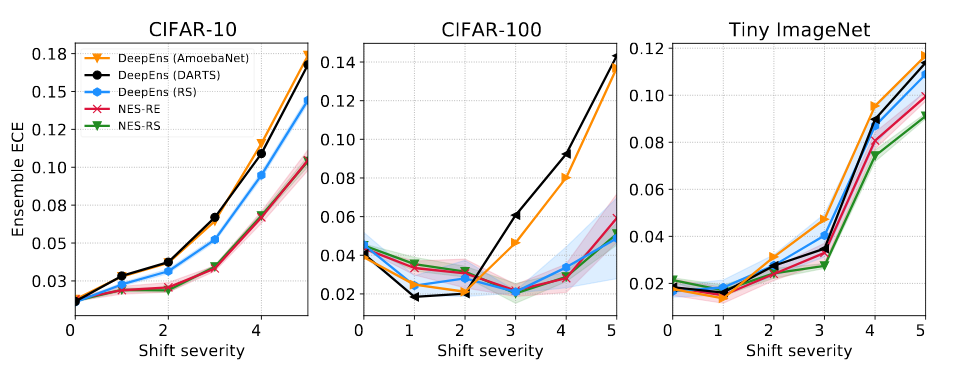
We assume that one does not have access to data points with test-time shift at training time, but one does have access to some validation data with a validation shift, which encapsulates one’s belief about test-time shift. Crucially, test and validation shifts are disjoint. A simple way to adapt NES algorithms to return ensembles robust to shift is by using the shifted validation data whenever applying forward step-wise selection. Note that in NES-RE we also use the shifted validation data whenever applying forward step-wise selection (Select ensemble in the figure). At each iteration of NES-RE we simply sample one of the clean or shifted validation sets in order to explore architectures that work well both in-distribution and during shift. To construct the shifted datasets we apply the common corruptions from Hendrycks et al. (see figure below).
Measuring the quality of uncertainty
We pick the following metrics to assess the uncertainty quality of our NES ensembles when compared to deep ensembles of a fixed architecture:
- Expected Calibration Error (ECE) — measures how well predicted confidence (probability of correctness) aligns with the observed accuracy
- Negative Log Likelihood (NLL)
- Classification error
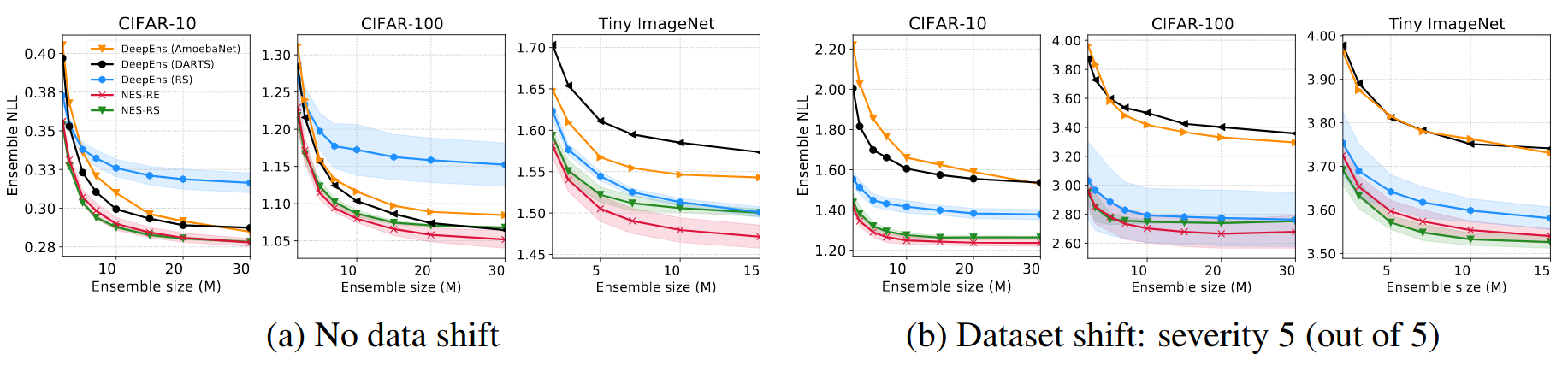
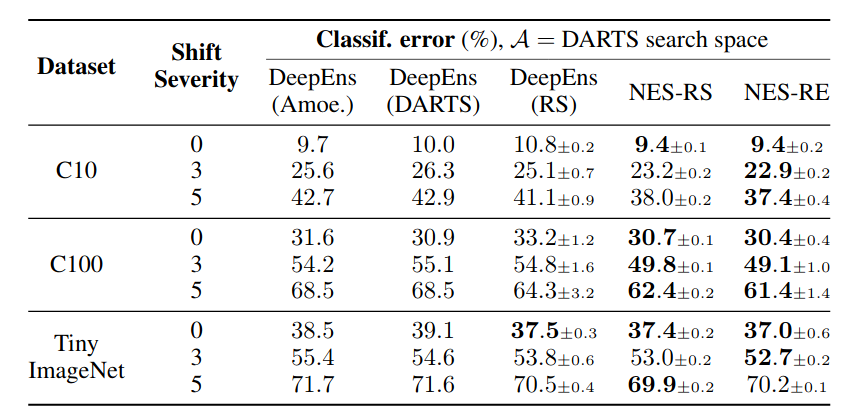
We compare NES to deep ensembles of architectures found using state-of-the-art NAS methods on the DARTS cell search space on standard image classification benchmarks. The results in the figures and table below show that NES algorithms are typically better than the deep ensemble baselines, in terms of NLL, calibration and classification error.
NES vs. deep ensembles of the global minimum
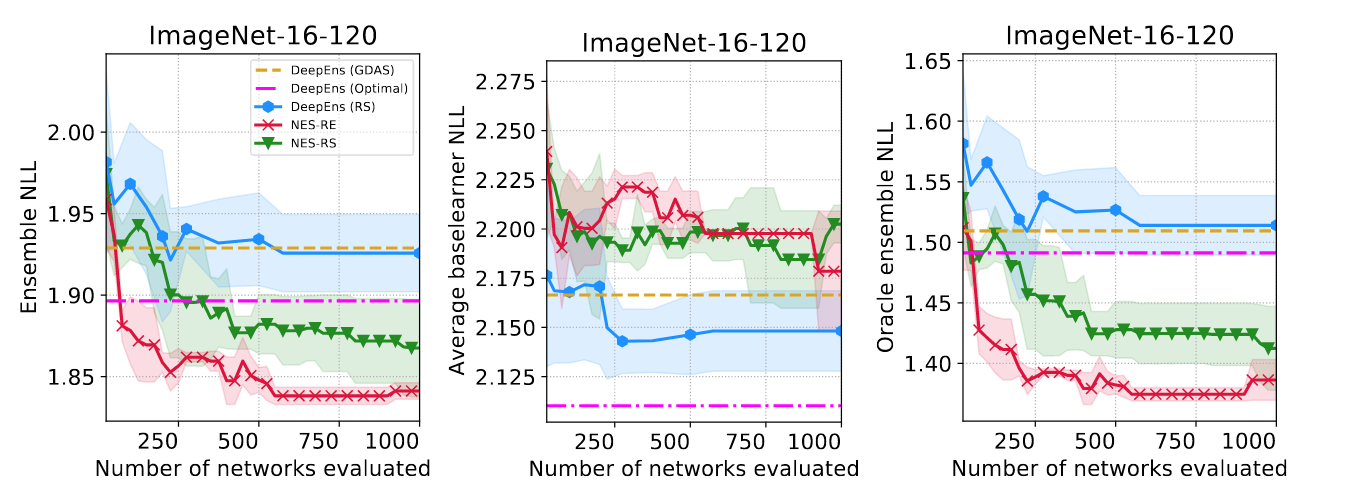
Next to the DARTS search space, we evaluate NES algorithms also on the NAS-Bench-201 search space. NAS-Bench-201 is a tabular NAS benchmark which consists of an exhaustively evaluated search space, i.e. with around 15k fully trained and evaluated architectures. Evaluating ensembles on this benchmark has multiple advantages:
- The parameters of the trained networks are already saved, therefore to obtain predictions we only need to do a forward pass.
- We know the global minimum in the space.
- We can run any NAS algorithm and obtain the optimized architecture quickly.
The figure below shows the ensemble NLL, average base learner NLL (the average NLL of the individual networks in the ensemble) and the oracle ensemble NLL (which for every input image returns the smallest loss across the ensemble base learner). As a rule of thumb, smaller oracle ensemble loss indicates more diverse base learner predictions (see right figure). Interestingly, we can see from the figure (left) that both NES-RS and NES-RE ensembles outperform the deep ensemble composed of the fixed global minimum architecture (DeepEns (Optimal); picked based on the validation loss), even though the individual base learners in DeepEns (Optimal) are stronger (middle figure).
Summary
Neural ensemble search introduces a so-far-untapped dimension of neural architecture search: finding networks that can be combined into a strong ensemble. We’ve showed that this approach yield better performance and uncertainty calibration than deep ensembles of the same fixed architecture. Neural Ensemble Search (NES) algorithms offer an automatic way of finding such architectures that optimize for ensemble performance and eventually yield more diverse ensembles, without ever explicitly defining diversity. In the future, we hope to improve the efficiency of NES algorithms even further, e.g. by employing ideas from one-shot neural architecture search.
Interested in more details and additional experiments? Check out our paper on arXiv.