By
Understanding and Robustifying Differentiable Architecture Search
Optimizing in the search of neural network architectures was initially defined as a discrete problem which intrinsically required to train and evaluate thousands of networks. This of course required huge amount of computational power, which was only possible for few institutions. One-shot neural architecture search (NAS) democratized this tedious search process by training only one large “supergraph” subsuming all possible architectures as its subgraphs. The NAS problem then boils down to finding the optimal path in this big graph, hence reducing the search costs to a small factor of a single function evaluation (one neural network training and evaluation). Notably, Differentiable ARchiTecture Search (DARTS) was widely appreciated in the NAS community due to its conceptual simplicity and effectiveness. In order to relax the discrete space to be continuous, DARTS linearly combines different operation choices to create a mixed operation. Afterwards, one can apply standard gradient descent to optimize in this relaxed architecture space.
In practice, DARTS works well for many common benchmarks for image classification and language modelling. However, this is not always the case. In early stages of our work we noticed that DARTS often has a tendency to put much attention to parameterless operations. This often leads to the final architecture being much worse than even a randomly sampled one (see figure below for degenerate cells found by DARTS in four different search spaces with two operations choices per edge). We were also not the only ones to encounter this issue, but at least three other research groups had similar problems with DARTS. Intrigued by the complex nature of this problem, but also by the importance that DARTS has played in the past year in the NAS community, we decided to go towards the path of answering the question of when and why does DARTS manifest such behavior in many scenarios.
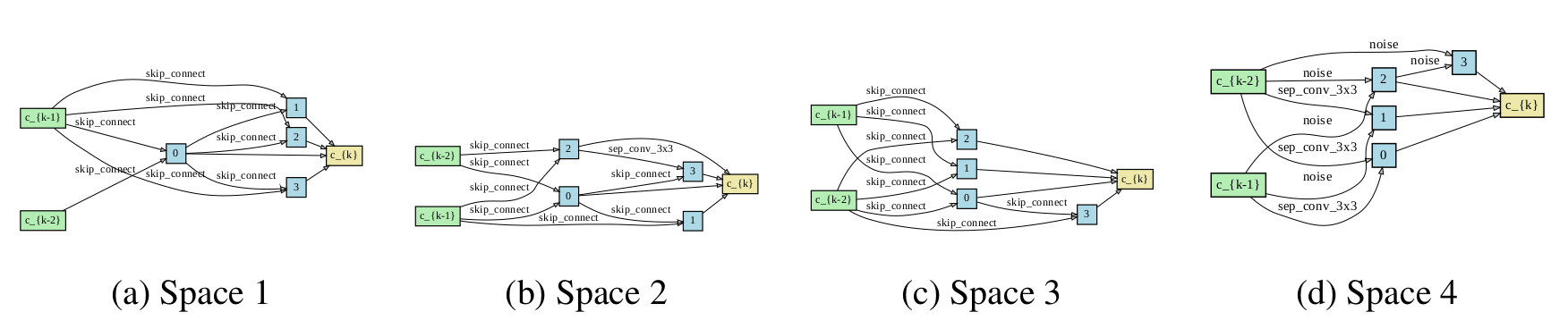
Figure caption: The degenerate normal cells standard DARTS finds on spaces S1-S4. For all spaces, DARTS chooses mostly parameter-less operations (skip connection) or even the harmful Noise operation.
Architecture Overfitting
In order to have a closer look at the architecture search process, we exhaustively evaluated a really small search space with a total number of 81 possible architectures. Afterwards, we ran DARTS on this search space, and at each epoch in time we queried the optimal architecture as assessed by DARTS from the tabular benchmark we evaluated before.
As the plot below shows, DARTS manages to find an architecture close to the global minimum around epoch 25, but later on the test regret of the architecture deemed optimal suddenly increases (due to the high attention DARTS focuses on parameterless operations, such as identity mappings, max pooling, etc.), even though the validation error of the search model converges to a low value. This clearly shows that there is an overfitting pattern manifesting in the architectural level. Of course, one simple strategy to avoid this overfitting would be to train and evaluate the architecture deemed to be optimal at each epoch on a separate set of data than the one used to optimize the architectural parameters, but this would be impractical for most of the cases. Below we will show an early stopping heuristic for DARTS which we propose in the paper, that keeps the search costs to the same level and is able to avoid architecture overfitting.
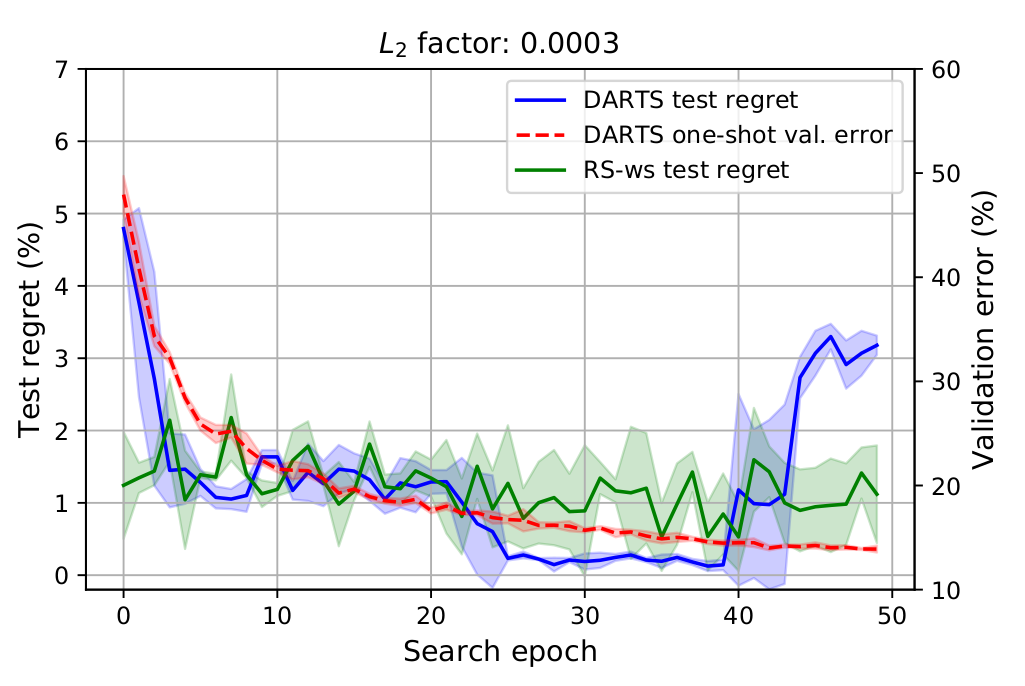
Figure caption: Test regret and validation error of the search model when running DARTS on the small search space and CIFAR-10. DARTS finds the global minimum but starts overfitting the architectural parameters to the validation set in the end.
Large Curvature and Generalization of Architectures
Having a differentiable objective in the architecture space allows one not only to use gradient-based methods to optimize the architecture, but also to obtain information about the curvature, smoothness, etc., of this objective function. Motivated by the work done in understanding the relation between optimization landscapes of neural networks and their generalization properties (e.g., in the case of small vs. large batch size training in normal supervised learning), we investigated whether the same pattern shows in the architectural parameters case.
The answer is YES. We compute the exact Hessian of the validation loss objective w.r.t. the architectural parameters on a randomly sampled mini-batch, and the results show that whenever the architecture search process starts degenerating, the dominant eigenvalue of this Hessian matrix also starts increasing (as shown in the animation below). We propose DARTS-ES (Early Stopping), which computes the dominant eigenvalue of the Hessian after each epoch and decides if the architecture optimization process should stop if the eigenvalue starts increasing rapidly. Our results show improvement compared to DARTS in all 12 settings we evaluated these algorithms.
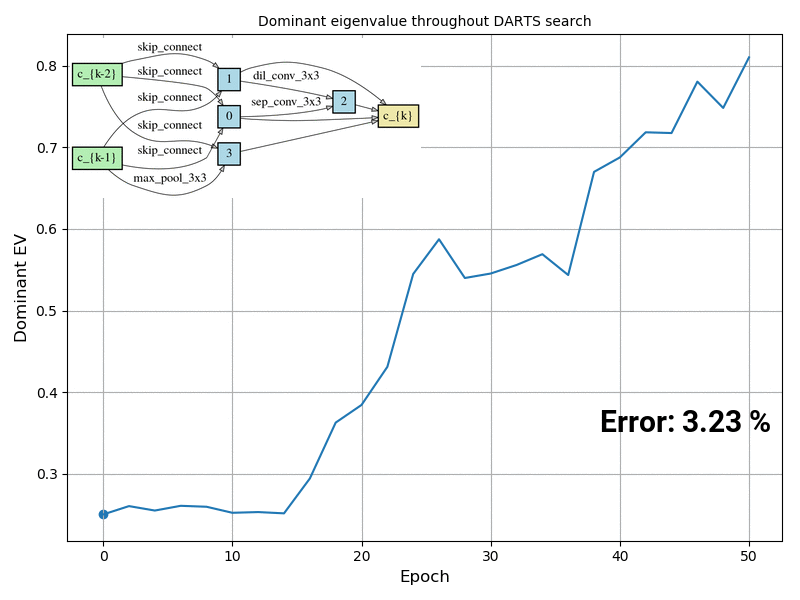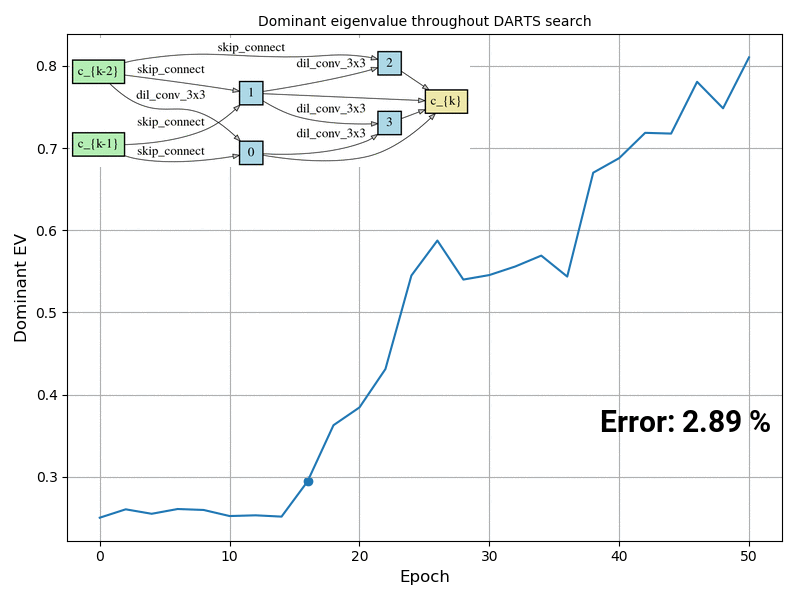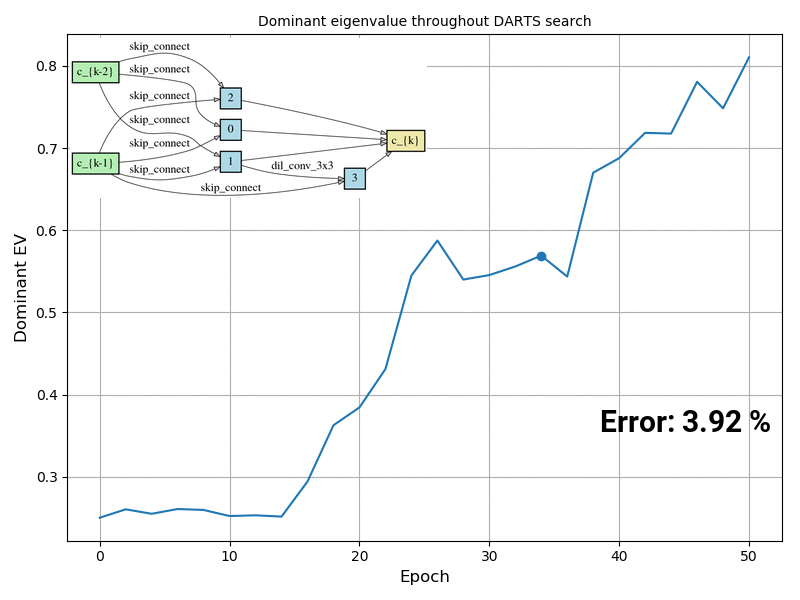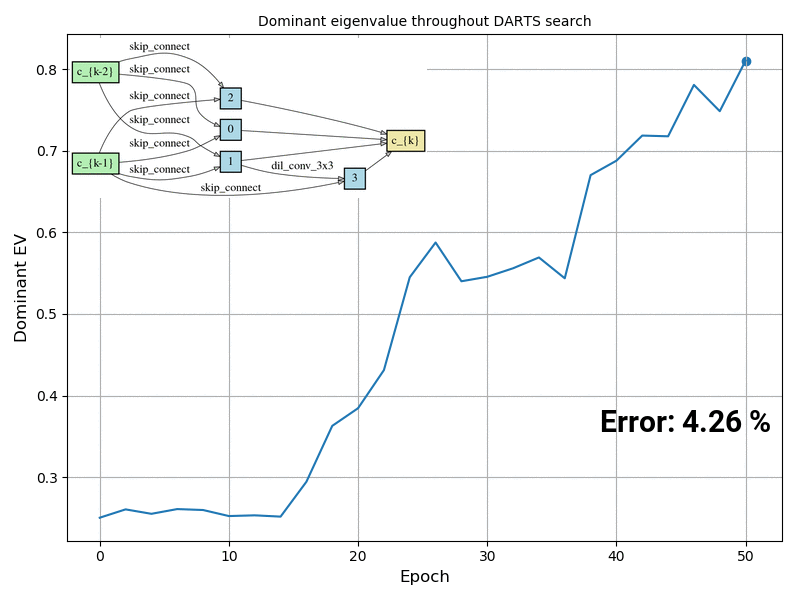
Figure caption: Visualization of the dominant eigenvalue of the Hessian of the validation loss w.r.t. the architectural parameters during DARTS search, and the normal cell together with the test error if that architecture at that point was retrained from scratch using the default DARTS evaluation settings. The experiment was conducted on CIFAR-10.
Adaptive Regularization based on objective curvature
DARTS optimization is treated as a bi-level optimization problem, with the validation and training loss as the outer and inner objectives, respectively. Theoretically speaking, the bi-level problem is guaranteed to converge to the global minimum of the outer objective if the inner objective is convex. This motivated us to investigate the effect of a stronger convex term in the training loss objective of DARTS. We firstly show the effect of a larger L2 regularization factor by evaluating DARTS’ search procedure from the beginning, with higher values than the default one used in the paper. As shown in the figure below, a stronger regularization factor helps DARTS to avoid these bad regions in the architecture space. Furthermore, by adaptively increasing the regularization factor based on the curvature information, we provide a new procedure (DARTS-ADA) that makes the architecture search process more robust to the hyperparameter initialization.
We conduct experiments with CIFAR-10, CIFAR-100 and SVHN for image classification, and with FlyingThings3D and Sintel for disparity estimation using Auto-DispNet (which uses the DARTS optimization algorithm to search for encoder-decoder architectures for dense prediction tasks). Our results are consistent across all these scenarios and also when using higher data augmentation strength instead of increasing the L2 factor.
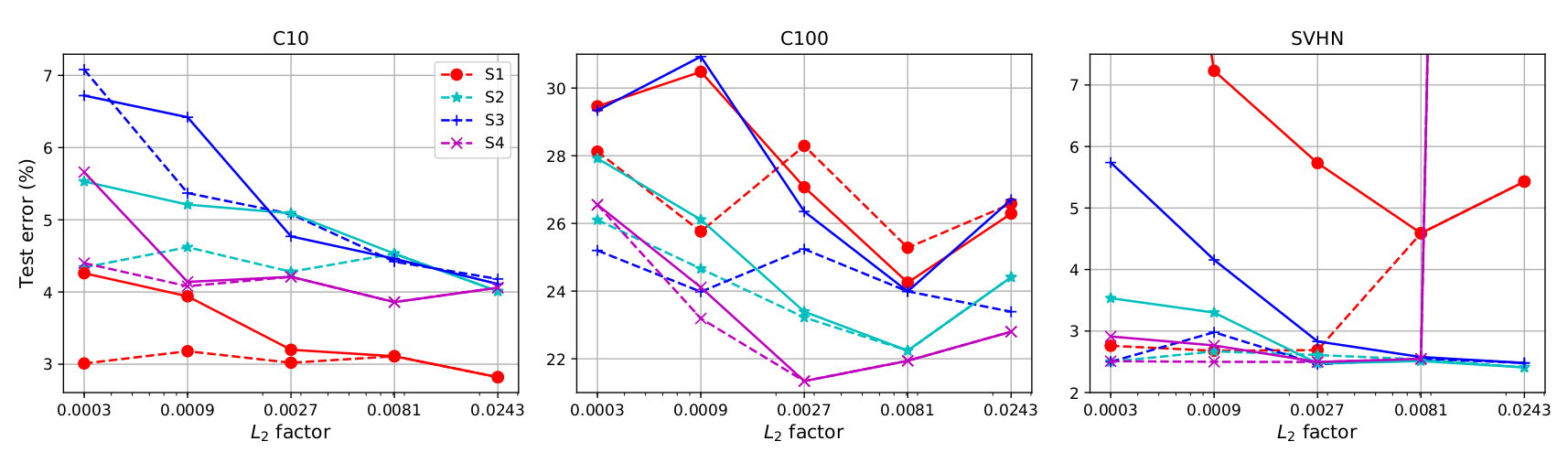
Figure caption: Effect of more regularization via L2 regularization during the DARTS search phase, on the test performance of the architectures discovered by DARTS and DARTS-ES. The results are presented for each of the search spaces S1-S4 and for CIFAR-10, CIFAR-100 and SVHN. The solid lines correspond to DARTS, the dashed lines to DARTS-ES.
How come the curvature of the architecture objective tells us about the generalization of the found architectures?
In order to answer this question, we have to keep in mind that what DARTS is optimizing is not the true objective (which would be a non-smooth function in the discrete space of architectures), but rather a relaxed smoothed version of it. Nevertheless, a discretization operator (argmax) is applied after the search has ended in order to obtain the “optimal” path from the input node to the output node in this graph representation of the space of neural networks.
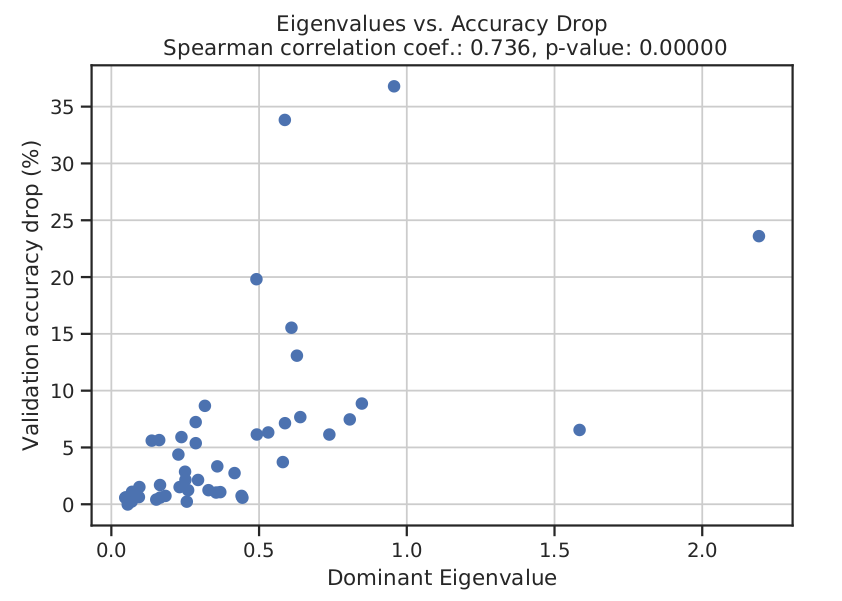
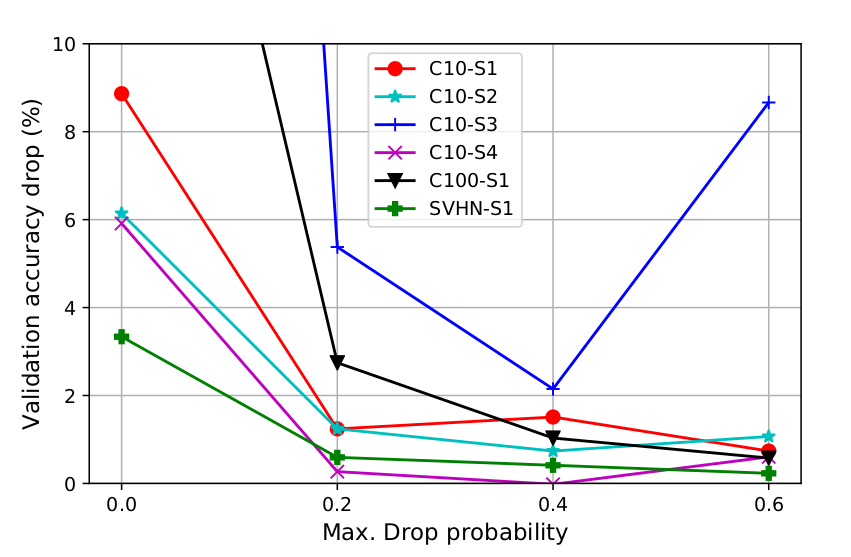 Figure caption: Drop in accuracy after discretizing the search model. (Left) Correlation with the landscape curvature. (Right) Example of some of the settings.
Figure caption: Drop in accuracy after discretizing the search model. (Left) Correlation with the landscape curvature. (Right) Example of some of the settings.
Intuitively enough, this discretization step in the architecture space will make performance worse. If the original relaxed architecture is in a sharper region of the objective it is more likely that this discretization step will make the objective value much worse compared to the case of a flatter landscape. In our paper, we empirically show that this is indeed the case; whenever the curvature is sharper the absolute difference between the validation error before and after the discretization step is larger (see plots below).
Take-home message
We believe that in order to develop a robust and effective optimizer, one has to understand what is happening in the low level behind the curtains, by both evaluating the method on several diverse benchmarks and by also getting more careful insights of the optimization dynamics and convergence. Our paper is a particular example where the failure mode of a method led towards a better understanding of the method and to the development of more robust versions of it. We hope that researchers reading this post will reconsider putting more effort in answering such questions of scientific interest, rather than merely trying to obtain new state-of-the-art results by incremental advances.
Interested in more details? Check out the paper. Also see a list of our other recent NAS papers.